Верификация программы
Верификация программы Борей 3D проводилась на аналитическом решении задачи о промерзании грунта [1]. Полученные численные результаты также, сравнивались с численными результатами Я. А. Кроника [2] и результатами аналитического решения распределения температуры по глубине, приведенными А. В. Лыковым [3].
Верификация программного обеспечения РН-НТЦ и СИ ГИОНК
Специалистами ООО «НК «Роснефть» — НТЦ» (РН-НТЦ) и специализированного института «Геотехнических исследований объектов нефтегазодобычи в криолитозоне на базе ООО «НК «Роснефть» — НТЦ» (СИ ГИОНК) выполнено сравнение результатов расчета температур грунтов на программном обеспечении (ПО) Борей 3D с аналитическим решением задачи Стефана. Для этого специалисты РН-НТЦ» выполнили расчет температур грунтов по аналитическим зависимостям [4]. Исполнители от РН-НТЦ Зелёный А.С. и Гилёв Н.Г.
Постановка задачи
Расчет распределения температур при промерзании грунта в течение 100 лет. Начальная температура грунта +2 °С. На верхней поверхности грунта поддерживается постоянная температура -1 °C.
В качестве грунта принималась супесь со следующими свойствами: ρd = 1.69 т/м3, Wtot = 0.21 д.е., Wm = 0.14 д.е., Ip = 0.01 д.е., Itot = 0.24 д.е., Dsal = 0.0752%.
По физическим свойствам супеси были рассчитаны следующие теплофизические свойства: Cth = 2.57 МДж/(м3*C), Cf = 2.05 МДж/(м3*C), λth = 1.76 Вт/(м*С), λf = 1.87 Вт/(м*С), Tbf = — 15 ⁰С, Qf = 118,89 МДж/м3
Боковые и нижняя поверхность грунта теплоизолированы, поэтому на этой поверхности принимается равенство теплового потока нулю. Шаг ячеек разностной сетки принимается 0,1 м с постоянной разбивкой до 30 м и с последующим равномерным увеличением шага по глубине, до глубины 250 метров.
Сравнение результатов расчета велось на периоды : 1 месяц; 1 год; 5 лет; 20 лет; 50 лет; 100 лет.
Результаты
Полученное численное решение задачи о промерзании грунта сравнивается с точным аналитическим решением данной задачи [4]. Результаты сопоставления показывают, что погрешность определения температуры не превышает 0,1 ⁰С. Вывод температур в программе Борей 3D осуществлялся с округлением до 2-го знака после запятой.
Сопоставление решений, полученных в программе Борей 3D, с точным аналитическим решением приведено в таблице 1 и на рисунках 2 и 3.
Таблица 1. Результаты расчета температур грунта на ПО Борей 3D.
| Глубина | 01.01.2018 | 01.02.2018 | 01.01.2019 | 01.01.2023 | 01.01.2038 | 01.01.2068 | 01.01.2118 |
|---|---|---|---|---|---|---|---|
| 0 | 2,00 | -1,00 | -1,00 | -1,00 | -1,00 | -1,00 | -1,00 |
| -0.1 | 2,00 | -0,66 | -0,89 | -0,95 | -0,98 | -0,98 | -0,99 |
| -0.2 | 2,00 | -0,32 | -0,77 | -0,90 | -0,95 | -0,97 | -0,98 |
| -0.3 | 2,00 | -0,09 | -0,66 | -0,85 | -0,93 | -0,95 | -0,97 |
| -0.4 | 2,00 | 0,00 | -0,55 | -0,81 | -0,90 | -0,94 | -0,96 |
| -0.5 | 2,00 | 0,10 | -0,43 | -0,76 | -0,88 | -0,92 | -0,95 |
| -1 | 2,00 | 0,56 | -0,08 | -0,51 | -0,76 | -0,85 | -0,89 |
| -1.5 | 2,00 | 0,97 | 0,06 | -0,27 | -0,64 | -0,77 | -0,84 |
| -2 | 2,00 | 1,30 | 0,20 | -0,12 | -0,52 | -0,70 | -0,78 |
| -5 | 2,00 | 1,98 | 0,94 | 0,26 | -0,05 | -0,24 | -0,46 |
| -10 | 2,00 | 2,00 | 1,70 | 0,82 | 0,26 | 0,03 | -0,09 |
| -20 | 2,00 | 2,00 | 1,99 | 1,59 | 0,82 | 0,42 | 0,19 |
| -50 | 2,00 | 2,00 | 2,00 | 2,00 | 1,79 | 1,33 | 0,94 |
| -100 | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | 1,93 | 1,70 |
| -250 | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 |
Таблица 2. Результаты расчета температур грунта по аналитическому решению задачи Стефана [4].
| Глубина | 01.01.2018 | 01.02.2018 | 01.01.2019 | 01.01.2023 | 01.01.2038 | 01.01.2068 | 01.01.2118 |
|---|---|---|---|---|---|---|---|
| 0 | 2,0000 | -1,0000 | -1,0000 | -1,0000 | -1,0000 | -1,0000 | -1,0000 |
| -0.1 | 2,0000 | -0,6316 | -0,8926 | -0,9520 | -0,9760 | -0,9848 | -0,9893 |
| -0.2 | 2,0000 | -0,2639 | -0,7852 | -0,9040 | -0,9520 | -0,9696 | -0,9785 |
| -0.3 | 2,0000 | -0,0824 | -0,6779 | -0,8559 | -0,9280 | -0,9544 | -0,9678 |
| -0.4 | 2,0000 | 0,0150 | -0,5706 | -0,8079 | -0,9040 | -0,9393 | -0,9571 |
| -0.5 | 2,0000 | 0,1113 | -0,4634 | -0,7599 | -0,8800 | -0,9241 | -0,9463 |
| -1 | 2,0000 | 0,5689 | -0,0908 | -0,5201 | -0,7599 | -0,8482 | -0,8926 |
| -1.5 | 2,0000 | 0,9685 | 0,0509 | -0,2806 | -0,6400 | -0,7723 | -0,8390 |
| -2 | 2,0000 | 1,2946 | 0,1902 | -0,1210 | -0,5201 | -0,6964 | -0,7853 |
| -5 | 2,0000 | 1,9784 | 0,9370 | 0,2547 | -0,0572 | -0,2419 | -0,4635 |
| -10 | 2,0000 | 2,0000 | 1,6949 | 0,8192 | 0,2547 | 0,0266 | -0,0909 |
| -20 | 2,0000 | 2,0000 | 1,9944 | 1,5866 | 0,8191 | 0,4133 | 0,1900 |
| -50 | 2,0000 | 2,0000 | 2,0000 | 1,9984 | 1,7880 | 1,3286 | 0,9366 |
| -100 | 2,0000 | 2,0000 | 2,0000 | 2,0000 | 1,9984 | 1,9250 | 1,6946 |
| -250 | 2,0000 | 2,0000 | 2,0000 | 2,0000 | 2,0000 | 2,0000 | 1,9997 |
Таблица 3. Абсолютное отклонение температур грунта рассчитанных по численным и аналитическим решениям.
| Глубина | 01.01.2018 | 01.02.2018 | 01.01.2019 | 01.01.2023 | 01.01.2038 | 01.01.2068 | 01.01.2118 |
|---|---|---|---|---|---|---|---|
| 0 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
| -0.1 | 0,0000 | 0,0284 | 0,0026 | 0,0020 | 0,0040 | 0,0048 | 0,0007 |
| -0.2 | 0,0000 | 0,0561 | 0,0152 | 0,0040 | 0,0020 | 0,0004 | 0,0015 |
| -0.3 | 0,0000 | 0,0076 | 0,0179 | 0,0059 | 0,0020 | 0,0044 | 0,0022 |
| -0.4 | 0,0000 | 0,0150 | 0,0206 | 0,0021 | 0,0040 | 0,0007 | 0,0029 |
| -0.5 | 0,0000 | 0,0113 | 0,0334 | 0,0001 | 0,0000 | 0,0041 | 0,0037 |
| -1 | 0,0000 | 0,0089 | 0,0108 | 0,0101 | 0,0001 | 0,0018 | 0,0026 |
| -1.5 | 0,0000 | 0,0015 | 0,0091 | 0,0106 | 0,0000 | 0,0023 | 0,0010 |
| -2 | 0,0000 | 0,0054 | 0,0098 | 0,0010 | 0,0001 | 0,0036 | 0,0053 |
| -5 | 0,0000 | 0,0016 | 0,0030 | 0,0053 | 0,0072 | 0,0019 | 0,0035 |
| -10 | 0,0000 | 0,0000 | 0,0051 | 0,0008 | 0,0053 | 0,0034 | 0,0009 |
| -20 | 0,0000 | 0,0000 | 0,0044 | 0,0034 | 0,0009 | 0,0067 | 0,0000 |
| -50 | 0,0000 | 0,0000 | 0,0000 | 0,0016 | 0,0020 | 0,0014 | 0,0034 |
| -100 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0016 | 0,0050 | 0,0054 |
| -250 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0003 |
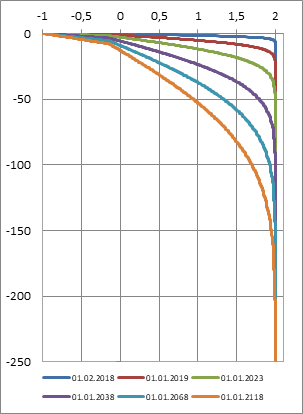
a) численное решение
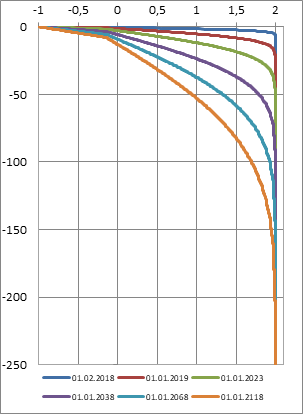
б) аналитическое решение
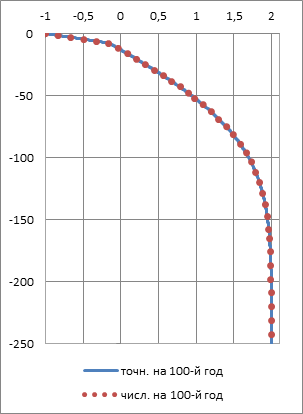
в) сопоставление численного и аналитического решения.
Рисунок 1. Результаты численного и аналитического решения.
Сравнение с численными результатами
Постановка задачи
Численные результаты, полученные с использованием программы Борей 3D, сравнивались с численными результатами Я. А. Кроника [2] и результатами аналитического решения распределения температуры по глубине, приведенными А. В. Лыковым [3] (так называемой задачи Стефана).
Промоделируем процесс промерзания влажного слоя песчаного грунта во времени с учетом фазовых переходов воды в интервале отрицательных температур, рассмотренный Я. А. Кроником [2]. На поверхности грунта задана постоянная температура Tsurf = – 5 °С. В начальный момент решения температура песчаного грунта по глубине составляет 0°С, а влажность слоя w = 0,20. В данной модели промерзающего грунта при сравнении результатов численного и аналитического решения температура начала замерзания принималась Tbf = -0,3 °С.
Результаты
В общем виде погрешность численных расчетов очень невелика (не превышает 2%) и при уменьшении шага по времени или размеров ячейки разностной сетки уменьшается.
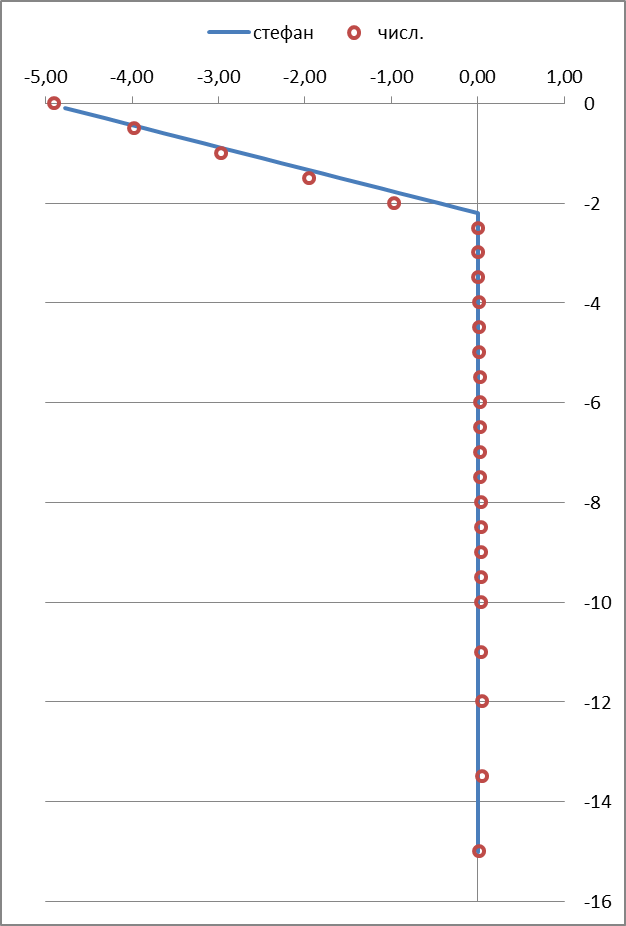
1-й год
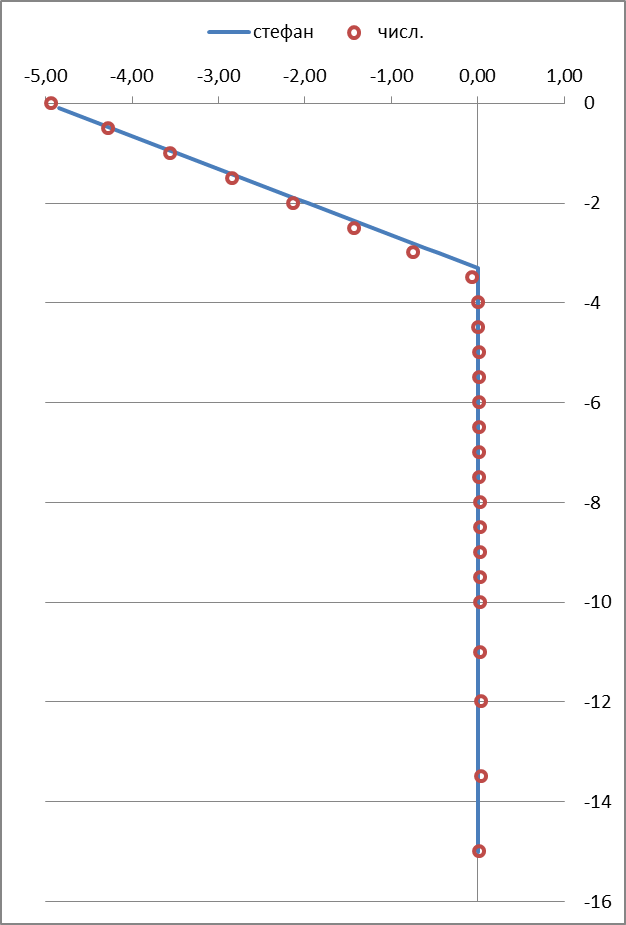
2-й год
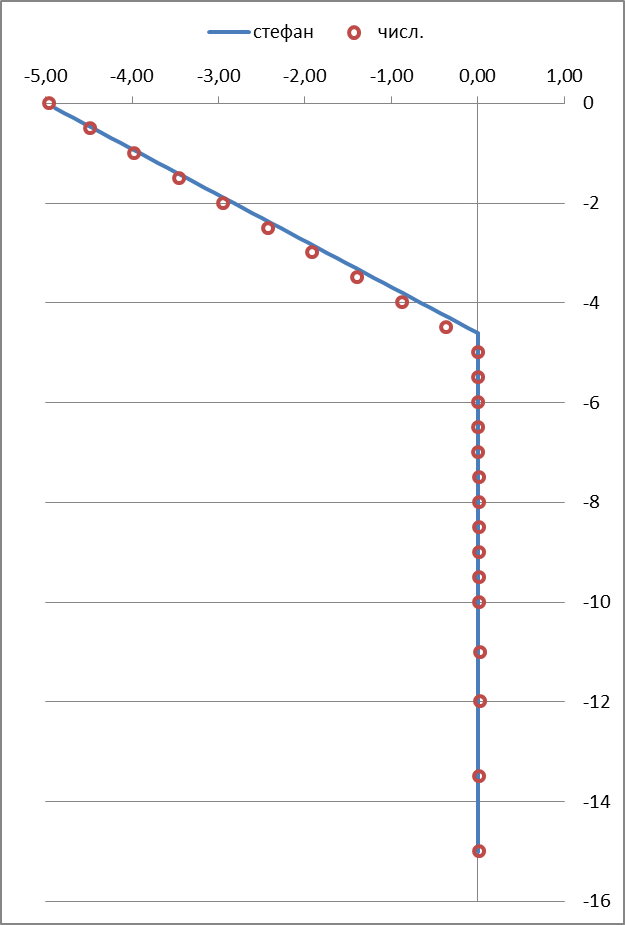
4-й год
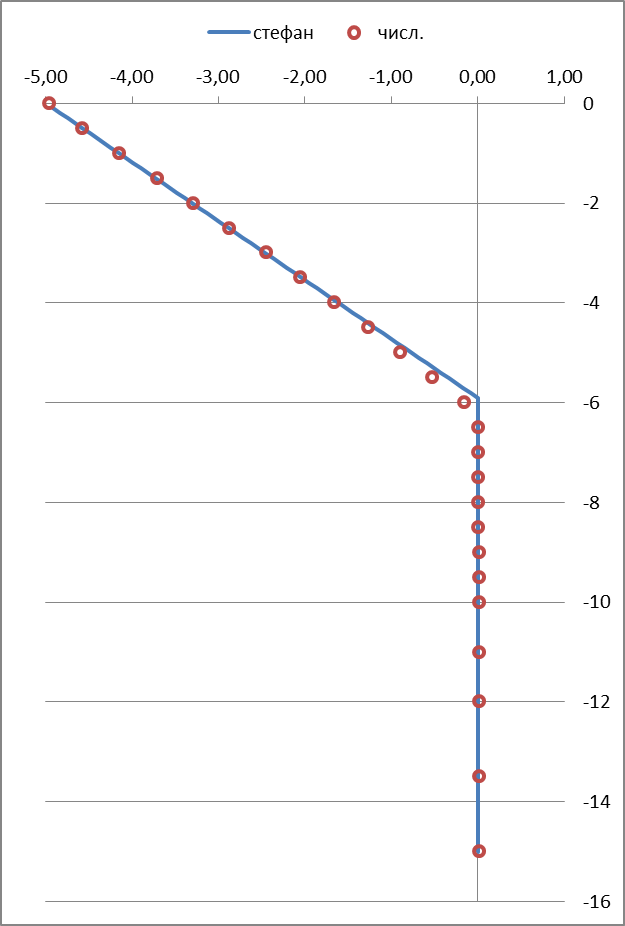
6-й год
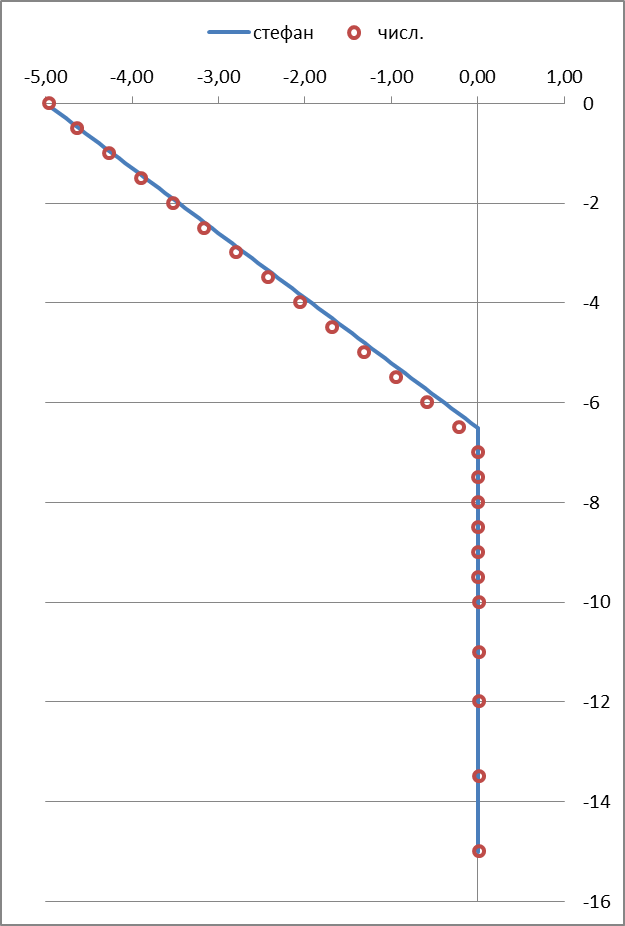
8-й год
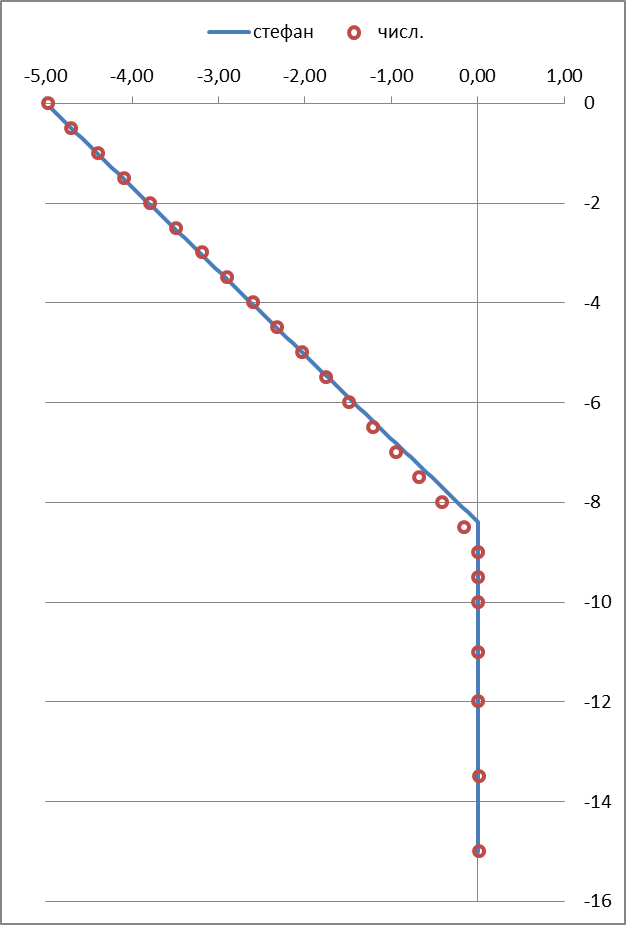
12-й год
Рисунок 2 – Результаты вычислительного эксперимента
Примечание: По оси абсцисс отложены температуры °С, по оси ординат — глубина, м.
Использованные источники:
- Кислицын А.А., Шабаров А.Б. Тепломассообмен. – Тюмень: ТГУ, 2007.
- Кроник Я. А., Демин И. И. Расчеты температурных полей и напряженно-деформированного состояния грунтовых сооружений методом конечных элементов: Учеб. пособие / МИСИ. М., 1981. 102 с.
- Лыков А. В. Теория теплопроводности. М: Высшая школа, 1967. 336 с.
- Кислицын А.А., Основы теплофизики (Лекции и семинары). – Тюмень: ТГУ, 2002.
